INTRODUCTION

Simulation studies in education, psychology, econometry, engineering, and statistics have been increasing in line with the advancements in technology. Especially for the cases where real data cannot be obtained, simulation, which is generating data by imitating it, is a commonly used option. When a case is analyzed using artificial data that display the qualities of the real data which is imitated are called simulation, Model sampling or Monte Carlo (Rubinstein, 1981). Monte Carlo method is the one that focuses on the relationship between simulation studies and chance and probability variables (Sobol, 1971).

Monte Carlo technique is comprised of the phases to identify the conditions that define a situation and to develop a model to reflect this specific situation. In this method, to obtain the data for the determined conditions of the situation that can reflect it, each independent variable is seperately repeated \(N\) times to generate \(N\) different sample groups. Because of this aspect, Monte Carlo method is also called statistical trial method. The effectiveness of Monte Carlo method depends on acquiring the data sets that pose the determined qualities; thus, variance value should be minimized by increasing iteration number (Sobol, 1971; Yaşa, 1996). Generating too many independent samples in Monte Carlo method could be related to Central Limit Theory. According to this theory, the average value of the \(N\) number samples taken from a population with average \(\mu\) and \(\sigma^{2}\) variance will display normal distribution with average \(\mu\) and \(\sigma^{2}/N\) variance.

Since Monte Carlo method requires to form samples that display the same characteristics and represent the same population and thus, the same conditions, it could be said that this method is related to Central Limit Theory. Let’s assume that there are \(N\) number of variables (\(\xi_{1}\), \(\xi_{2}\), \(\xi_{3}\), …, \(\xi_{N}\)) that have the same probability distribution. These will have the same expected value (\(E\xi_{1} = m\)) and also the same variance (\(V\xi = b^{2}\)). This could be explained mathematically as follows (Sobol, 1971):

\[E\xi_{1} = E\xi_{2} = \ldots = E\xi_{N} = m\]

\[V\xi_{1} = V\xi_{2} = \ldots = V\xi_{N} = b^{2}\]

If the sum of chance variables is defined with \(\rho_{N}\);

\[\rho_{N} = \xi_{1} + \xi_{2} + \ldots + \xi_{N}\]

The expected value of this equation is (\(E\)) and the varience is (\(V\))

\[E\rho_{N} = E\left( \xi_{1} + \xi_{2} + \ldots + \xi_{N} \right) = Nm\]

\[V\rho_{N} = V\left( \xi_{1} + \xi_{2} + \ldots + \xi_{N} \right) = Nb^{2}\]

According to central limit Theory, to determine any interval \((a',\ b')\) in a normal distribution with the same parameters (\(a = Nm\) and \(\sigma^{2} = Nb^{2}\)), the following formula is used:

\[P\left\{ a^{'} < \rho_{N} < b' \right\} \approx \int_{a'}^{b'}{P\xi_{N}(x)dx}\]

This means that the sum of \(N\) number of identical variables \(\rho_{N}\) will be approximately normal. However, it is also stated that the same result can be obtained even when all the included chance variables are not identical and independent. In Monte Carlo method, on the other hand, a chance variable \(E\xi = m\) is tried to be reached in order to obtain an \(m\) value. Also, \(N\) number of independent variables \(\xi_{1}\), \(\xi_{2}\), \(\xi_{3}\), …, \(\xi_{N}\) that are identical with \(\xi\) their distribution is analyzed as \(V\xi = b^{2}\) is accepted. If \(N\) is large enough, its sum of distribution \(\rho_{N} = \xi_{1} + \xi_{2} + \ldots + \xi_{N}\) will be approximately normal due to the Central Limit Theory and \(a = Nm\) and \(\sigma_{2} = Nb^{2}\) parameters will be obtained. Accordingly;

According to \(P\left\{ a - 3b\sqrt{N} < \zeta < a + 3b\sqrt{N} \right\} = 0.997\) normal distribution equation,

It is \(P\left\{ Nm - 3b\sqrt{N} < \rho_{N} < Nm\ + 3b\sqrt{N} \right\} \approx 0.997\)

When both sides of the equation are divided by \(N\), the following equation is obtained and the probablity does not change.

\[P\left\{ m - 3b\sqrt{N} < \rho_{N}/N < m + 3b/\sqrt{N} \right\} \approx 0.997\]

This equation can also be written as:

\[P\left\{ \left| \left( 1/N \right)\sum_{j = 1}^{N}\zeta_{j} - m \right| < 3b/\sqrt{N} \right\} \approx 0.997\]

and formula is obtained. This formula is of great importance in Monte Carlo method since it not only represents the calculation of \(m\), but also contains the prediction of error. Considering chance, when \(N\) number of \(\xi\) chance variables are sampled and when one single value is defined for \(\xi_{1}\), \(\xi_{2}\), …, \(\xi_{N}\) values, all distributions will be similar. The mean value of these values will be almost equal to \(m\). The error of this approach will not exceed \(3b/\sqrt{N}\) value. This indicates that as \(N\), the number of samples, increases, the error will get closer to zero (Sobol, 1971).

Obtaining low error estimation in Monte Carlo method by increasing the number of iteration brings with it widespread use in many fields such as statistics, economy, and education. Given the practical difficulties of conducting applications on large groups in education field, it is inevitable to make use of simulative data in various examinations on the test theories. Regarding the situations where it is appropriate to use the Monte Carlo method, The Psychometric Society (1979) states that it is a method to be applied when determination of sample distribution, comparison of test and item statistics or estimators are targeted, and in situations where it is difficult to obtain the desired conditions in real data, and when comparison of algorithms under different conditions is aimed. When using the Monte Carlo method, the first thing to do is determine the conditions of the model to be established (Hoaglin and Andrews, 1975; Naylor, Balintfy, Burdick, and Chu, 1968). The steps to be followed in using this technique are summarized by Harwell, Stone, Hsu, and Kirisci (1996):

• Research questions based on the aim of the study is determined

• Variables and their conditions (levels) are defined

• Appropriate experiential design is developed

• Data reflecting the determined conditions is generated based on a test theory

• Parameters are estimated

• Comparative analysis is conducted

• This is repeated for each cell in the design

• The obtained results are evaluated both inferentially and descriptively. These findings will also provide the answers to the research questions.

In the articles published in Applied Psychological Measurement (APM), Psychometrika, and Journal of Educational Measurement (JEM) journals between 1994 and 1995, approximately one in the fourth to one in the third of them used Monte Carlo method (Harwell et al., 1996). In 2018, simulation method was used in 39 articles out of 46 original research articles published in Psychometrika; in 6 articles out of 13 original research articles published in two issues of Educational Measurement: Issues and Practice except for special issues, in 35 articles out of 40 original research articles published in Applied Psychological Measurement, in 22 articles among the 30 articles published in Journal of Educational Measurement. National Council on Measurement in Education (NCME) reports that 91 studies presented in 2018 were simulation studies. In 2019, 77 of the studies reported in their abstracts to be simulation studies, Monte Carlo studies or stated that they used simulative data in their studies. These studies often explore test equalization, structural equalizing model, Generalizability Theory, CCT, CAT, and IRT while item and test parameters estimated were compared.

While some simulation studies give explanation only on what the manipulated variables are, others explain simulation process in detail. For example, in the first two issues of Journal of Educational Measurement in 2019, there are 18 original research papers published. Out of these, 13 have used simulated data and only seven of them provide information regarding the number of iteration. In these studies, 100 (Svetina, Ling Liaw, and Rutkowski, 2019; Wind and Jones, 2019; Zhang, Wang, and Shi, 2019) and 200 (Wolkowitz, 2019) it has been reported to have generated data through iteration. In literature, there are studies using different iteration number such as 10000 (Saeki ve Tango, 2014), 1000 (Kannan, Sgammato, Tannenbaum and Katz 2015; Bionis, Huang and Gramacy, 2019), 500 (Glen Satten, Flanders and Yang, 2001) 100 (Fay and Gerow; 2013), 10 (Kéry and Royle, 2016; Murie and Nadon, 2018). On the other hand, there are also simulation studies that have not used iteration or reported iteration number (Hambleton, Jones and Rogers, 1993; Harwell and Janosky, 1991; Hulin, Lissak and Drasgow, 1982; Qualls and Ansley, 1985; Yen, 1987). Not using iteration in simulation studies brings the risk of having high sample variance, obtaining higher or lower values that the expected parameter estimates and having low reliability in the results obtained. In order to obtain values close to the determined parameter estimates, in other words to decrease variance value, increasing iteration number is the most appropriate method (Hammersly and Handscombe, 1964; Lewis and Orav, 1989).

Mundform, Schaffer, Kim, Shaw, and Thongteeraparp (2011) state that there is no procedure to determine the number of iterations in the simulation studies, so the number of iterations is at the discretion of the researcher. Inadequate number of iterations in the data generation phase leads to errors in estimations and so, the power of the Monte Carlo method is increased by the number of iterations (Brooks, 2002; Hutchinson and Bandalos, 1997; Gifford and Swaminathan, 1990; Stone, 1993; Hammersly and Handscombe, 1964; Lewis and Orav, 1989). In fact, in the Monte Carlo simulation studies, increasing the number of iterations enables to produce data with less error estimation, but there is no clear explanation regarding how many iterations should be conducted (Hutchinson and Bandalos, 1997). Considering the fact that simulation studies are frequently applied nowadays, the results obtained from these studies reflect the real situation directly and it is directly related to the simulation process, so it can be stated that the number of iterations plays an important role. At this point, it is thought that identifying the number of iterations required in MC simulation studies and by which variables it is affected will guide the researchers. In this study, the aim is to determine the number of iterations required in Monte Carlo simulation studies based on IRT and to determine the variation of test and item parameters depending on the number of iterations. For this purpose, two different simulation studies were conducted. The first simulation study was conducted without limiting the parameters of the item. In the second simulation study, the condition of limiting the parameters of the item was discussed.

METHOD

The study aims to determine how many iterations numbers are needed in MC simulation studies based on IRT models and to track the changes in item and test parameters depending on different iterations numbers. MC simulation method was used in order to determine the mentioned values, and thus, the study is a simulation study.

The aims of the study were sought through conducting two simulation studies. The main variable tested in terms of its effect on test and item parametres was iterations number; and therefore, iterations number was differentiated in both simulation studies as iterations number 5, 10, 25, 50, 100, 250, 500, 1000 and 10000. In literature, the possible relationship between iterations number and sample size is explained in relation to Central Limit Theory (Sobol, 1971). In order to determine the required iterations number depending on the sample size, the sample size (500, 1000 and 3000) was determined as a variable in both simulation studies. Considering the claim that increasing iterations number will decrease errors, the changes in the standard error of the parameter estimates based on different iterations numbers were determined in the first simulation study. It is thought that adding qualities and applying limitations to the data to be generated in Monte Carlo simulation studies will affect the performance of the simulation. In order to determine the required iterations number when one parameter value was limited, item parameter values were limited in the second simulation study. Based on IRT 3-parameter model, the required number of iterations for the condition when one item parameter was limited (b), when two of them were limited (b and a) and when the three of them were limited (b, a ve c) were determined by attaining intervals for each separately. Item number was determined to be 10 for the first simulation study and 20 for the second study. Comparing the results from both of these simulation studies, the changes in iterations number based on item number were investigated.

For data generation and analysis for the study, R program (2011), ltm package was used. To investigate the required iterations number, the standard error of the estimate of the item parameter, the sum of test information, and model data fit parameters were considered in the first simulation study while estimates of the item parameters, the sum of test information, and model data fit parameters were considered in the second simulation study. G² method was used to determine Model data fit. G², is one of the methods used to define model data fit based on \(- 2\log\lambda\) difference statistics with data sets scored in 1-0 (Dais, 2006). When comparing G² ratios, determining which model fits which data or which data fits which model could be done using significance test (Andersen, 1973; Baker and Kim, 2004; Bock and Aitkin, 1981).

Simulation Study -1-

The first Monte Carlo simulation study was conducted following the steps listed in Table 1 and using R program in ltm package.

Result of simulation study -1-

The results obtained from the first simulation study are presented by firstly using the item parameters and then the test parameters. The results of the item parameter estimation obtained based on step 6 as shown in Table 1 and the results of test information and model data fits are displayed below and the results are evaluated respectively.

 

Table 1. The Phases of Monte Carlo Simulation Study Phase Action 1. Research questions based on the aim of the study are determined What is the effect of IRT iterations numbern in Monte Carlo method on; Test parameters? Item parameters? How many iterations are sufficient in Monte Carlo IRT Simulation studies? 2. Variables and their conditions (levels) are defined. Samples: 500, 1000 and 3000 Number of Items: 10 Respond category 2 (1-0) Iteration number 5, 10, 25, 50, 100, 250, 500, 1000 and 10000 3. Appropriate experiential design is developed With sample sice condition × item number condition × iteration number condition = 3 × 2 × 9 = 54 different simulations were conducted. 4. Data reflecting the determined conditions is generated based on a test theory. Based on Item Response Theory one dimensional 3 Parameters Logistics Model, experiential scenarios with determined conditions were created using simulative data. 5. Parameters are estimated Item parametres: The standard error values of item difficulty, item discrimination and chance parametres’ estimates were predicted. Test parameter: Total test value and the fit of each data set with the model were estimated through -2logλ . 6. Comparative analysis is conducted Item and test parameters estimated from the data sets were compared under the same conditions but with different iteration numbers. For example; The item and test parameters estimated from the condition with 500 sample size and item number of 10, but simulated using 5, 10, 25, 50, 100, 250, 500, 1000 and 1000 iteration numbers were compared (as stated in phase 5) Descriptive evaluation was made to compare the standard error of item parameter and test information. As for evaluating model data fit, G2 ratio based on -2logλ  difference was used. 7. Repeating the process for all conditions For sample size condition × item number condition = 3 × 2 = 6. The comparisons stated in the 6th phase were conducted separately. 8. Evaluating the obtained results The obtained results are evaluated in line with the research questions.

 

Figure 1 presents the results for the change in the standard error of \(b\) parameter estimates based on different iteration numbers in the condition with no limitation on \(b\) parameter when the sample size is 500, 1000 and 3000. The results indicate that for all 10 items, the standard error of parameter estimates are fixed after 500 iteration number for 500 sample size, after 250 iteration number for 1000 and after 100 iteration number for 3000 sample size. Also, as iteration number increases, the standard error of \(b\) parameter estimate gets lower. Thus, this indicates that standard error gets lower as iteration number increases depending on the sample size and gets fixed after a specific point.

 

Figure 1. The change in standard error values regarding parameter b estimates based on iteration number

 

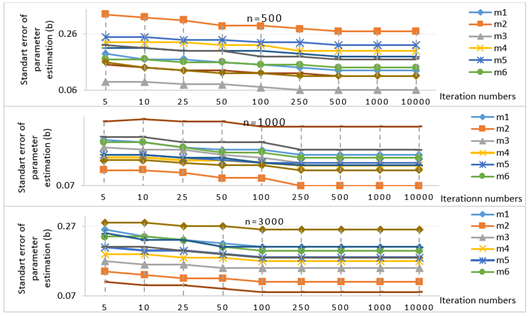
Figure 2 presents the results for the change in the standard error of a parameter estimates based on different iteration numbers in the condition with no limitation on parameter \(a\) when the sample size is 500, 1000 and 3000. Similar to the results obtained for parameter \(b\), it can be seen that the standard error of parameter \(a\) estimates is fixed after 500 iteration for 500 sample size, after 250 iteration for 1000 and after 100 iteration for 3000 sample size for all 10 items. Also, as iteration number increases, the standard error of parameter \(a\) estimate gets lower in all three sample sizes. Therefore, it can be claimed that standard error gets lower as iteration number increases depending on the sample size and is fixed after a specific point.

 

Figure 2. The change in standard error values regarding parameter a estimates based on iteration number

 

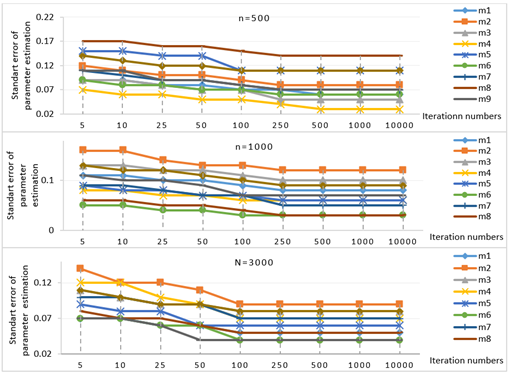
Figure 3 shows the results for the change in the standard error of parameter \(c\) estimates based on different iteration numbers in the condition with no limitation on parameter \(c\) when the sample size is 500, 1000 and 3000. Similarly, the standard error of parameter \(c\) estimates are fixed after 500 iteration for 500 sample size, after 250 iteration for 1000 and after 100 iteration for 3000 sample size. As iteration number increases, the standard error of parameter \(c\) estimate gets lower in all three sample sizes. Similar results were obtained for three items’ parameters. As a result, it can be argued that as sample size increases, the standard error of parameter estimate gets lower and is fixed after 250 iteration when the sample size is 500, after 250 when it is 1000, and after 100 when the sample size is 3000. In addition, it can be concluded that iteration number that minimizes the parameter estimate depends on the sample size and it decreases as the sample size increases.

 

Figure 3. The change in standard error values regarding parameter c estimates based on iteration number

 

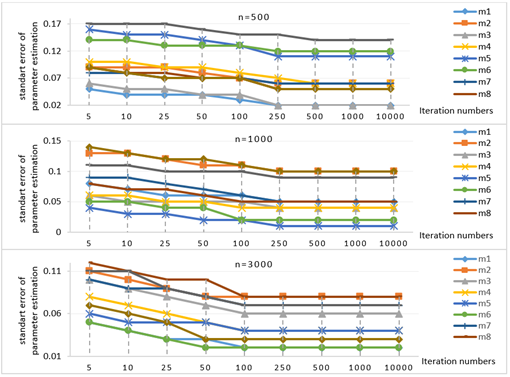
Figure 4 displays the change in the estimated sum of test information based on iteration number in each sample size.

 

Figure 4. The change in the sum of test information based on iteration number

 

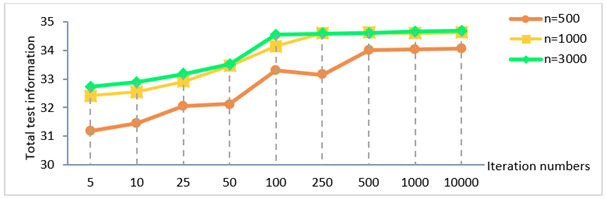
When the line graph in Figure 4 regarding the total test information change is examined, it is seen that as the number of iterations increases, the total test information increases and it is fixed after 500 iterations when sample size is 500, after 250 iterations when sample size is 1000, and it is fixed after 100 iterations when sample size is 3000. Accordingly, similar to the standard error of item parameter estimation, as the sample size increases, the number of iterations required decreases and the total test information increases to a certain point.

Table 2 presents the variation of the model data fit based on the number of iterations. Based on this, it is concluded that there is no significant difference in the model data fit after 500 iterations when the sample size is 500, after 250 iterations when the sample size is 1000 and after 100 iterations when the sample size is 3000, in other words, the model data fit is fixed. Accordingly, as the sample size increases, the number of iterations required to set the model data fit fixed decreases.

 

Table 2. The change in model data fit based on iteration mumber Iterations number N=500 N=1000 N=3000 –2 log λ G2 –2 log λ G2 –2 log λ G2 5 -2268.54   -5144.18   -11002.40   10 -2251.53 -17.01* -5124.10 -20.08* -10982.65 -19.75* 25 -2230.14 -21.39* -5092.74 -31.36* -10961.02 -21.63* 50 -2205.47 -24.67* -5041.08 -51.66* -10930.05 -30.97* 100 -2186.91 -18.56* -4988.19 -52.89* -10909.87 -20.18* 250 -2167.13 -19.78* -4967.55 -20.64* -10902.14 -7.73 500 -2143.41 -23.72* -4960.28 -7.27 -10894.91 -7.23 1000 -2134.08 -9.33 -4957.53 -2.75 -10891.12 -3.79 10000 -2128.64 -5.44 -4952.30 -5.23 -10889.52 -1.60 *p (χ2sd=9>16.92) <0.05

 

When the item and test parameters, which were estimated from the data produced by different iterations with 500, 1000 and 3000 sample sizes, are analyzed by fixing the number of items to 10, it was concluded that fixed estimates can be made by 500 iterations when sample size is 500, 250 iterations when sample size is 1000, 100 iterations when sample size is 3000. In other words, it can be said that the estimates obtained after these iterations did not differ, so these were the sufficient iterations. For instance, in the condition with a sample size of 1000, when the results obtained with 100 iterations and the results obtained with 250 iterations are compared, the less error of the parameter estimation from the data set is produced by the 250 iterations, the greater the total test information is and the data produced with 250 iterations is more compatible with the model. Therefore, it can be stated that producing data with 250 iterations will provide more accurate estimations, but under the same condition, when the data produced with 250 iterations and the data produced with 500 iterations are compared, the test and the item parameters do not change. Based on this, it is seen that in MC method, more accurate estimations can be made when the number of iterations is increased, but the number of iterations is effective up to a point and then the item and the test parameters will be fixed or there will be no significant difference. However, as the sample size increases, the number of iterations required decreases.

Simulation Study -2-

In the second simulation study, it was aimed to determine the required number of iterations and their effects in Monte Carlo method on the IRT test and item parameters when item parameters are limited: \(b\) value was limited between -2 logit and +2 logit, a parameter was limited between 1 and 1,5 and \(c\) parameter was limited between 0 and 0.20. The Monte Carlo simulation study was carried out using the ltm package of the R program according to the steps in Table 3.

 

Table 3. The Phases of Monte Carlo Simulation study Phase Action 1. Research questions based on the aim of the study are determined How many iterations are sufficient to obtain predefined item parameter intervals in IRT Simulation studies conducted using Monte Carlo method when item parameters were limited? 2. Variables and their conditions (levels) are defined. Sample Size: 500, 1000 and 3000 Number of Items: 20 Response Category 2 (1-0) Number of iteration 5, 10, 25, 50, 100, 250, 500, 1000 and 10000 Conditions for Item parameter limitation: • Condition with no limitation on any parameter • Condition when only b  parameter was limited, b  value was limited between -2 logit and +2 logit values and the other parameters were not limited. • Condition when a  and b  parametres were limited: b  value was limited between -2 logit and +2 logit while a  parameter was limited between 1 and 1,5 and c  parameter was not limited. • Condition when a , b  and c  parametres were limited: b  value was limited between -2 logit and +2 logit while a  parameter was limited between 1 and 1,5 and c  parameter was limited between 0 and 0.20. Accordingly, the condition with no limitation was compared with the condition with one parameter limited, with the condition with two parameters limited, and with the condition with three parameters limited in order to determine how manipulation impacted the required iteration number. 3. Appropriate experiential design is developed With sample size condition × item number condition × iteration number condition = 3 × 1 × 4 × 9 = 108 different simulations were conducted. 4. Data reflecting the determined conditions is generated based on a test theory. Based on Item Response Theory one dimensional 3 Parameters Logistics Model, experiential scenarios with determined conditions were created using MC model. 5. Parameters are estimated Item parametres: How many iterations were needed to obtain the intervals determined during data generation through estimating Item rigour, distinctiveness and chance parameters was defined. Test parameter: Total test value and the fit of each data set with the model were estimated through -2logλ . 6. Comparative analysis is conducted Item parameters estimated from the data sets were compared under the same condition but with different iteration numbers. For example; the condition with 500 sample size and limitation on only parameter b  was simulated with 5, 10, 25, 50, 100, 250, 500, 1000 and 1000 iteration numbers and compared in terms of the required iteration numbers to reach the predefined intervals for parameter b . Descriptive evaluation was conducted to compare the standard error and test information. As for evaluating model data fit, G2 ratio based on -2logλ  difference was used. 7. Repeating the process for all conditions For sample size condition × parameter limitation condition = 3 × 3 = 9 the comparisons stated in the 6th phase were conducted separately. 8. Evaluating the obtained results The obtained results are evaluated in line with the aim of the study.

 

Result of simulation study -2-

Based on 3PLM, only parameter \(b\), parameters \(b\) and \(a\), and parameters \(b\), \(a\), and \(c\) were limited and the required iteration number was determined while the value change depending on the sum of test information and model data fit under these conditions was tracked in order to obtain the minimum and maximum values depending on the iteration number.

The changes observed as a result of different iteration numbers and the item and the test parameters obtained by generating 500, 1000, and 3000 sample sizes with different iteration numbers and without any limitation in the 20-item first condition are displayed as shown in Figure 5.

 

Figure 5. The change in item parameters based on iteration number in the condition without any limitation on item and test parameters

 

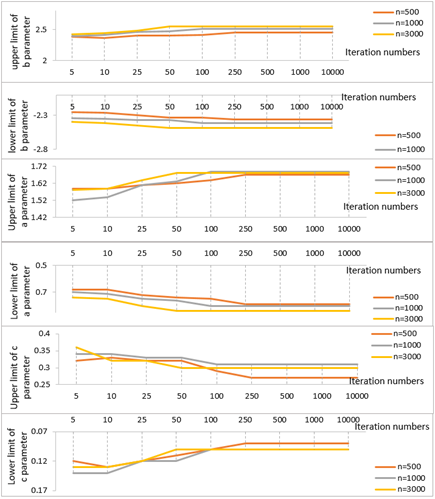
Figure 5 shows the changes of parametres \(a\), \(b\) and \(c\) based on iteration number. Accordingly, all three item parameters get fixed after 250 iterations for 500, 100 iterations for 1000 and 50 iterations for 3000 sample size. Thus, this indicates that iteration number gets lower as the sample size increases.

The sum of test results obtained from the data using different iteration numbers but having no limitations on item and test parameters are displayed in Figure 6.

 

Figure 6. The change in the sum of test information based on iteration number in the condition without any limitation on item and test parameters

 

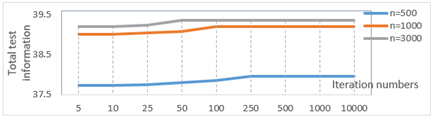
According to Figure 6, it is seen that, similar to the results for item parameters, the sum of test information is fixed after 250 iterations for 500, 100 iterations for 1000 and 50 iterations for 3000 sample size. Table 4 presents the change in model data fit based on iteration number in this condition.

When the change in model data fit based on iteration number presented in Table 4 is analyzed, the model data fit is fixed after 250 iterations and more for 500, 100 iterations and more for 1000 and 50 iterations and more for 3000 sample size. It is also observed that there is no statistically significant difference among data sets based on model data fit.

 

Table 4. The change in model data fit based on iteration number in the condition withouth any limitation on item and test parameters Iteration number N=500 N=1000 N=3000 –2 log λ G2 –2 log λ G2 –2 log λ G2 5 -4598.13   -8596.18   -16988.33   10 -4563.41 -34.72* -8558.02 -38.16* -16945.14 -43.19* 25 -4527.38 -36.03* -8522.6 -35.42* -16899.02 -46.12* 50 -4492.72 -34.66* -8479.25 -43.35* -16854.46 -44.56* 100 -4456.09 -36.63* -8438.73 -40.52* -16843.07 -11.39 250 -4419.40 -36.69* -8415.35 -23.38 -16831.58 -11.49 500 -4411.88 -7.52 -8404.08 -11.27 -16825.13 -6.45 1000 -4402.08 -9.80 -8395.41 -8.67 -16821.80 -3.33 10000 -4935.25 -6.83 -8388.54 -6.87 -16818.19 -3.61 *p (χ2sd=19>30.14) <0.05

 

Figure 7 presents the results regarding minimum and maximum values of a parameter estimated from the data generated by different iteration numbers in the second scenario where parameter \(b\) was limited between -2 logit and +2 logit and where parameters \(a\) and \(c\) had no limitations.

 

Figure 7. Estimates of parameter b in the condition where only parameter b had limitation

 

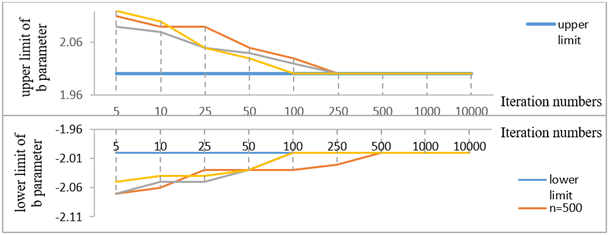
When determining the minimum and maximum value estimates, the range of 20=item \(b\) parameter values were considered. For example, parameter \(b\) was estimated in the condition 1000 sample size and 100 number of iterations and the highest \(b\) value was above 2 (the determined maximum value was +2 logit) while the lowest \(b\) value was -2 (the minimum value determined at data generation scenario). Accordingly, when the sample size is 1000, 100 iterations is not sufficient since the determined boarders could not be reached. When the sample size is 1000, the minimum required iteration number is 250 with which the determined parameter \(b\) range, or the minimum and maximum values, could be reached. Therefore, the minimum required iteration number for this condition is 250. When the sample size is 500, minimum 500 iterations are required and when it is 3000, minimum 100 iterations are necessary in order to reach the targeted parameter intervals.

The change in the sum of test information depending on iteration number in the condition with limitation on only parameter \(b\) estimates is presented in Figure 8.

 

Figure 8. The change in the sum of test information depending on iteration number in the condition with limitation on only parameter b

 

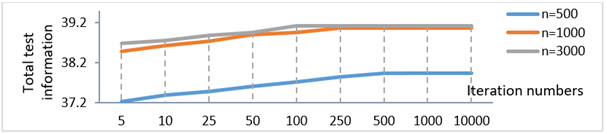
When analyzing the change in the sum of test information depending on iteration number in the condition with limitation on only parameter \(b\), it is observed that test information increases as iteration number increases and that test information does not change after 500 iterations for 500 sample size, after 250 iterations for 1000 sample size and after 100 iterations for 3000 sample size.

 

Table 5. The change in model data fit based on iteration number in the condition with limitation on only parameter \(b\) Iteration number N=500 N=1000 N=3000 –2 log λ G2 –2 log λ   –2 log λ G2 5 -4612.40   -8640.13   -17392.15   10 -4575.87 -36.53* -8529.75 110.38* -17360.01 -32.14* 25 -4533.45 -42.42* -8494.33 35.42* -17318.42 -41.59* 50 -4501.16 -32.29* -8455.86 38.47* -17287.38 -31.04* 100 -4469.43 -31.73* -8419.43 36.43* -17251.10 -36.28* 250 -4429.92 -39.51* -8385.04 34.39* -17229.68 -21.42 500 -4391.09 -38.83* -8376.61 8.43 -17205.13 -24.55 1000 -4374.61 -16.48 -8355.02 21.59 -17190.53 -14.60 10000 -4368.15 -6.46 -8349.79 5.23 -17186.81 -3.72 *p (χ2sd=19>30.14) <0.05

 

When analyzing the change in model data fit based on iteration number in the condition with limitation on only parameter \(b\), it is seen that there is no significant difference in model data fit after 500 iterations for 500 sample size, after 250 iterations for 1000 sample size, and after 100 iterations for 3000 sample size. Therefore, these iteration numbers could be accepted to be necessary and sufficient.

In the third scenario, for the condition limited (from -2 logit to +2 logit) for parameter \(b\) and (from 1 to 1.5) for parameter \(a\), the results regarding the changes in parameters \(a\) and \(b\) depending on iteration number and the required iteration numbers to reach the determined value intervals are shown in Figure 9.

 

Figure 9. The change in parameters a and b based on iteration number as a result of the limitations on parameters a and b

 

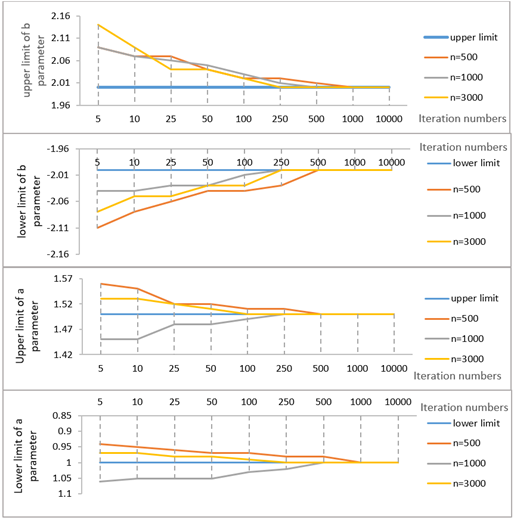
Analyzing Figure 9, it can be seen that the predefined intervals during data generation could be obtained for both \(a\) and \(b\) parameters with 1000 iterations when the sample size is 500, with 500 iterations when the sample size is 1000, and with 250 iterations when the sample size is 3000.

The change in test information based on iteration number is presented in Figure 10.

 

Figure 10. The change in test information based on iteration number in the condition with limitations on parameters a and b

 

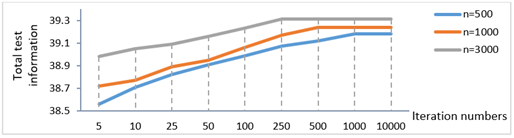
When the results regarding the change in test information based on iteration number in the condition with limitations on parameters \(a\) and \(b\) are analyzed, fixation is achieved with 1000 iterations when the sample size is 500, with 500 iterations when the sample size is 1000, and with 250 iterations when the sample size is 3000.

Table 6 presents the results of the change in model data fit in different iteration numbers when parametres \(a\) and \(b\) were limited. Accordingly, it can be seen that model data fit is fixed with 1000 iterations when the sample size is 500, with 500 iterations when the sample size is 1000, and with 250 iterations when the sample size is 3000.

 

Table 6. The change in model data fit in different iterations numbers (when parametres \(a\) and \(b\) are limited) Iteration number N=500 N=1000 N=3000 –2 log λ G2 –2 log λ   –2 log λ G2 5 -4516.85   -8559.70   -17212.44   10 -4482.51 -34.34* -8526.23 33.47* -17180.10 32.34* 25 -4437.80 -44.71* -8488.55 37.68* -17135.86 44.24* 50 -4402.96 -34.84* -8448.14 40.41* -17102.22 33.64* 100 -4362.11 -40.85* -8405.37 42.77* -17067.46 34.76* 250 -4325.84 -36.27* -8370.33 35.04* -17025.27 42.19* 500 -4277.08 -48.76* -8331.01 39.32* -16999.07 26.20 1000 -4239.23 -37.85* -8305.80 25.21 -16981.92 17.15 10000 -4221.78 -17.45 -8297.44 8.36 -16969.13 12.79 *p (χ2sd=19>30.14) <0.05

 

Figure 11 displays the results regarding the change in the values of estimated parameters based on different iteration numbers in the fourth scenario with the condition where parameters \(a\), \(b\), and \(c\) were limited and the required iteration numbers.

 

Figure 11. The changes in parametres a, b and c based on iteration numbers in the condition where parameters a, b, and c were limited

 

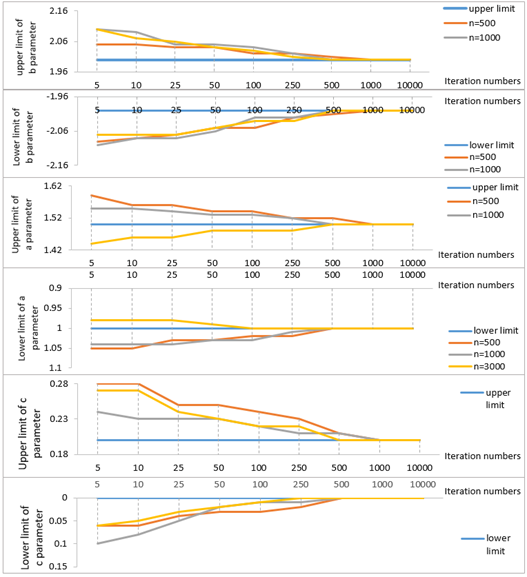
When the changes in parametres \(a\), \(b\) and \(c\) based on iteration numbers and the iteration numbers required to reach the minimum and maximum values determined during data generation are analyzed, the targeted value could be achieved for all three item parameters with 1000 iterations when the sample size is 500 and 1000, and with 500 iterations with 3000 sample size.

Figure 12 displays the results for the sum of test information based on iteration number in the conditions with limitations on parameters \(a\), \(b\), and \(c\). According to the results, test information is fixed with 1000 iterations when the sample size is 500 and 1000, and with 500 iterations when the sample size is 3000; and also, test information increases as the iteration number increases upto this point.

 

Figure 12. The changes in the sum of test information based on iteration number in the condition with limitations in parameters a, b, and c

 

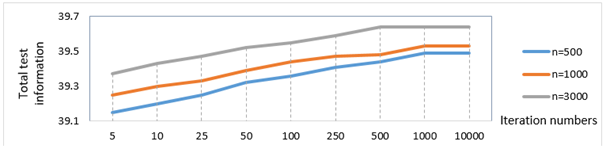
In Table 7, the change in model data fit based on iteration number in the condition with limitations on parameters \(a\), \(b\) and \(c\). The results show that there are no significant differences in model data fit after 1000 iterations when the sample size is 500 and 1000, and after 500 iterations when the sample size is 3000.

 

Table 7. The change in model data fit in different iteration numbers (when parameters \(a\), \(b\), and \(c\) are limited) Iteration number N=500 N=1000 N=3000 –2 log λ G2 –2 log λ   –2 log λ G2 5 -4344.15   -8586.44   -17202.08   10 -4309.88 34.27* -8543.19 43.25* -17158.57 43.51* 25 -4264.09 45.79* -8505.90 37.29* -17114.40 44.17* 50 -4211.16 52.93* -8459.07 46.83* -17079.45 34.95* 100 -4175.11 36.05* -8404.63 54.44* -17015.81 63.64* 250 -4118.83 56.28* -8372.17 32.46* -16971.27 44.54* 500 -4068.72 50.11* -8329.75 42.42* -16933.54 37.73* 1000 -4030.01 38.71* -8290.10 39.65* -16922.18 11.36 10000 -4013.43 16.58 -8298.88 11.22 -16909.05 13.13 *p (χ2sd=19>30.14) <0.05

 

In the data production phase, when the estimation of the limited item parameters and the number of iterations that reached to the target value are examined, it is seen that as the number of limited parameters is increased, the number of iterations required to reach the values determined for the parameters increases as well. For example, in the case of a sample size of 500, when only parameter \(b\) is limited, 250 iterations are required, when parameters \(a\) and \(b\) are limited, 500 iterations, and finally when parameters \(a\), \(b\) and \(c\) are limited, 1000 repeptioins are obtained as the parameter ranges specified. Accordingly, as the number of manipulated variables increases during the data generation step, the number of iterations required increases. Another relationship revealed by the research findings is between sample size and number of iterations. As the sample size increases, the number of iterations required decreases. For instance, for the condition in which only parameter \(b\) is restricted, to reach the specified ranges 500 iterations are needed when the sample size is 500 and 100 iterations are required when the sample size is 3000. Thus, when the sample size increases, the number of iterations required decreases. However, in a condition discussed, it is seen that all of the predicted parameters are fixed at the same number of iterations or the specified intervals are reached. It can be said that the use of item parameters is effective in estimating the IRT test parameters, and when the item parameters are fixed, the other parameters are fixed accordingly.

DISCUSSION

In this study, it is aimed at determining the variation of test and item parameters depending on the number of iterations when Monte Carlo simulation method, which is widely used in education field, based on IRT one dimensional three parameter logistic model is used, in addition to determining how the variation of test and item parameters depending on the number of iterations and the required number of iterations are affected when the parameters are manipulated. Applying two different simulation studies, the variation of item and test parameters in MC method depending on the number of iterations was identified.

In the first simulation study, the number of items in different sample sizes was fixed at 10 and the data were analyzed by generating them at different iterations without any restrictions on the item parameters. By reporting the variation of item parameter estimation based on the number of iterations of the standard error, the minimum number of iterations at which the error was reached and fixed was determined. Additionally, total test information and model data fit were estimated and the number of iterations of these parameters were also determined. The results of this study showed that when the sample size is 500, the required number of iterations is 500, when the sample size is 1000, the required number of iterations is 250 and when the sample size is 3000, the required number of iterations is 100. Based on this result, when the MC method is used in IRT studies, the required number of iterations decreases with the increasing sample size, and when the number of iterations is increased, estimations are gathered with fewer errors. By increasing the number of iterations, the data with higher test information and more model-fit-data can be obtained, but after the necessary and sufficient number of iterations, there is no significant difference in test and item parameter estimates. Thus, it will not be possible to state that the greater the number of iterations, the fewer are the errors.

In the second simulation study, item and test parameters were estimated with and without applying any limitations on item parameters by fixing the item number to 20 and by generating data suitable to MC method and 3PLM using different iteration numbers. In the condition without any limitations applyied on item parameters, the iteration number that gets item and test parameters fixed was determined. As for the condition with limitations applies on item parameters, the number of iteration required to obtain the defined parameter intervals was identified. Subsequently, the condition where item parameters were restricted and the one without any restrictions were compared in terms of their required iterationn number in order to determine the effect of manipulating parameters during data generation in MC method on the required number of iteration. As a result, it has been found that as the number of the manipulated variable, that is the parameter, increases, then the required number of iteration increases as well. In the condition without any limitations applied on parameters, it has been observed that data could be generated with 250 iteration when the sample size is 500, with 100 iteration when the size is 1000, and with 50 iteration when the sample size is 3000. When only one parameter was restricted during data generation, then the required iteration number is 500 when the sample size is 500, 250 iteration when the size is 1000, and 100 iteration when the sample size is 3000. In the case where two parameters were restricted during data generation, then the required iteration number is 1000 when the sample size is 500, 500 iteration when the size is 1000, and 250 iteration when the sample size is 3000. In the last condition where all item parameters were restricted, it has been observed that the required iteration number is 1000 when the sample size is 500, 1000 iteration when the size is 1000, and 500 iteration when the sample size is 3000. Moving from these findings, it can be claimed that as the number of manipulated variables increases during data generation, then the number of iteration required also increases. As the results of the first study indicates, the required iteration number decreases as the sample size increases. Table 8 presents the findings regarding the required iteration numbers identified under the determined conditions in both of the simulation studies.

 

Table 8. The required iteration numbers obtained in simulation studies   Sample Size (N) Item Number Limited Parameter Simulation study 500 1000 3000 Required iteration number 500 250 100 10 0 1 250 100 50 20 0 2 500 250 100 20 1 (only b) 2 1000 500 250 20 2 (a and b) 2 1000 1000 500 20 3 (a, b and c) 2

 

Binois, Huang, Gramary and Ludkovsk (2019), Gifford and Swaminathan (1990) and Harwell, Rubinstein, Hayes and Olds (1992) point out that the required number of iteration will decrease as the sample size increases. As Table 8 shows, the required number of iteration decreases in both simulation studies under all conditions as the sample size increases. Research results in the field argue that obtaining the desired intervals to be manipulated through simulation gets more difficult as the sample size gets smaller (Baker, 1998; Brown, 1994; Hulin, Lissak and Drasgow, 1982; Goldman and Raju, 1986; Lord, 1968). The results of the present research seems to support this claim. In both simulation studies and under all conditions, higher number of iteration was required to reach test parameters and fixed item while in larger samples, fewer iterations were required to get parameter estimates fixed.

Brooks (2002) and Hutchinson and Bandalos (1997) state that insufficient number of iterations will lead to misinterpretations (tahmin) and increase error. In the first simulation study, it is shown that standard errors in item parameter estimate decreased as the number of iteration increased. On the other hand, considering that test information in IRT provides estimates of reliability and validity and that test information keeps increasing to a specific point as iteration number is increased, it could be postulated that increasing iteration number in MC method will decrease error. Gifford and Swaminathan (1990) point out that more retriations are needed when the number of parameters and variables increase. According to the result of the second simulation study, as the number of variables determined and manipulated during data generation is increased, it is revealed that the necessary number of iterations increases as well. For example, when comparing the required number of iterations for each sample under condition one in the second simulation study and the required number in condition two, where only one item was restricted, it can be seen that restricting an item necessitates higher number of iterations.

Research in the field postulates that the required iteration number will decrease as the number of variables increase (Brooks, 2002; Hutchinson and Bandalos; 1997; Sobol, 1971). Accordingly, when comparing the condition with 10 item number in the first simulation study with the condition that has 20 item number and that is not restricted regarding item parameters, it would be expected that the condition with 10 item number would require lower iteration numbers. However, the results of the present study indicate that the condition with 10 item required higher number of iterations compared to the condition with 20 items. This could be the result of the model utilized. In the study, the data were generated and analyzed based on 3PLM model, which is one of the IRT unidimensional models. In this model, there is a unidimensional continuous variable. As a result, it could be claimed that MC method requires higher number of iterations if a quality is defined or a restriction is placed during data generation process in a way that the main hypothesis of the model chosen is not met. Therefore, it could be indicated that, in MC method, the required number of iterations is affected by whether the hypotheses of the model is met or not.

Mundform, Schaffer, Kim, Shaw and Thongteeraparp (2011) claim that there is no specific procedure for determining the number of iteration in simulation studies and that this is up to the researcher. Harwell and others (1992), on the other hand, state that the required number of iteration in MC method will depend on the model, the variable and the analyses to be conducted. Although the literature in the field has many studies conducted on MC applying different number of iterations, no study that gives a specific number for required iteration or that explains how iteration number impacts test and item parameters could be found. In the present study, it is concluded that the required number of iterations increases as the number of qualities sought is higher and that the number of iteration differs as the sample size, item number and the manipulated variable number differ. The required number of iterations determined in this study are the ones to be regarded when generating data in MC method under similar conditions.

SUGGESTIONS FOR FUTURE MC STUDIES

In the present study, the impact of iteration number on IRT parameters in the commonly used MC method was determined through one dimensional IRT 3PLM. The findings indicate that the more variables are considered and manipulated, the higher number of iterations will be necessary; therefore, when using MC method, researchers are advised to decide on iteration number considering the model’s parameters at hand and the number of variables to be manipulated. Considering the iteration numbers used in the studies in the field, it can be seen that these numbers will be insufficient. Obtaining estimates in MC method with close to reality or low error and reaching the targeted parameter levels depend on iteration number. Thus, iteration number is an important technical decision to be made in MC studies. It is clear that iteration number has an effect on estimate results in MC studies and the required iteration number depends on the number of conditions and their levels. The more complex is the simulated condition and the more qualities it possesses, the higher number of iterations will be necessary to obtain estimates without errors.

The present study investigates the relationship between number of retriations and test and item parameters in MC method based on unidimensional three-parameter model. Thus, it should be taken into consideration that number of retriations will differ in multi-dimensional or one-parameter models as it is also indicated as a result of the present study that the number of variables and the defined intervals impact the number of iteration. Furthermore, the present study focuses on IRT parameters. Similar studies could be carried out with CTT or G Theory parameters. Similarly this study focused on IRT 3PLM, similar studies could be carried out with other IRT models. A similar study could be done by limiting the item parameters at different ranges.