INTRODUCTION

Since Ball and her colleagues (e.g., Ball and Bass, 2009; Ball et al., 2009; Ball et al., 2008) proposed the framework of mathematical knowledge for teaching (MKT), researches on teachers’ knowledge in mathematical education have been highly oriented by MKT. Their established theory seems to answer the question of what kind of knowledge a mathematics teacher needs. They presented an elaboration of Shulman’s (1986) categorizations of pedagogical content knowledge (PCK) and subject matter knowledge (SMK); PCK consisted of knowledge of content and students, knowledge of content and teaching and knowledge of content and curriculum (KCC); SMK consisted of common content knowledge, specialized content knowledge and horizon content knowledge (HCK). Furthermore, they provided empirical evidence to support the existence of the six sub-domains in MKT, and further explained or defined the majority of these sub-domains. However, there were few explanations of what HCK meant and they merely provided ideas about HCK. It is reasonable to argue that maybe there are very limited opportunities to catch HCK in primary school level. Therefore, we attempted to analyze the high-school mathematics teaching based on mathematical approach under the framework of MKT, and exemplified some incidences to interpret mathematics teachers’ HCK from an elementary-to-advanced aspect, which complements Kline’s (1924) advanced-to-elementary one.

The work presented in this article is part of a project which aimed at studying Taiwanese experienced high-school mathematics teachers’ MKT. Three participant high-school mathematics teachers (Teacher A, Teacher B and Teacher C), each of whom have been teaching in a public high-school in northern Taiwan for more than 10 years, were purposefully selected for studying their MKT. Our research group consisted of an experienced teacher educator, four graduate students, and a retired consultant high-school mathematics teacher (Mr. Chiu), who had taught for more than 35 years in both public and private high schools and had been a committee member of the Taiwanese high-school mathematics curriculum design. The observed and videotaped units were chosen by Mr. Chiu, and the team watched and discussed three teachers’ videotapes together twice a week. In general, Mr. Chiu provided some suggestions based on the purpose of curriculum and student learning, or explained why certain mathematical tasks must be included in the curriculum. We, as usual, were discussing a problem task in Figure 1 (The Minimal Volume Problem) collected from the three teachers’ videotapes as the following:

Figure 1. The minimal value of volume of tetrahedron OABC

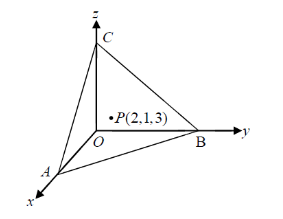
A plane E passes through P (2, 1, 3) and cuts the positive coordinate half-axes at points A, B and C, and O is the origin point,

1. Find the minimum value of the volume of the tetrahedron OABC, and

2. Determine the equation of the plane that cuts this least volume.

However, Mr. Chiu pointed out that high-school mathematics teachers must lead their students to explore a fundamental¹ characteristic of the point P; furthermore, he provided a teaching illustration based on his understanding of the advanced mathematics (about algebraic topology), and he explained and justified how his teaching practice could penetrate through the structure of mathematics to extend to or to connect to the advanced level. We then looked for the undergraduate and graduate mathematics and found that a fundamental characteristic of the point P can be mathematically extended to algebraic topology. Hence, we tried to understand whether these three participants would show different levels of the mathematical knowledge, and to explore how their different levels of the mathematical knowledge might be connected to their classroom teaching practice.

In this article, we describe the different level of the specific mathematical knowledge of the participant teachers and Mr. Chiu according to the different explorations or inquiries they used in classroom teaching, and then propose a complementary aspect about HCK in terms of the three teachers and Mr. Chiu’s teaching illustrations.

HCK-AN UNSOLVED PROBLEM

Agreement is widespread that teachers’ mathematical knowledge always plays a primary role in classroom teaching activity (Ball et al., 2008; Davis and Simmt, 2006; Zazkis and Momolo, 2011; Zazkis and Zazkis, 2011). Research on teacher’s mathematical knowledge used in teaching has developed significantly over the last two decades. However, perhaps the most prominent analytical structure is the MKT framework introduced by Ball and her colleagues. They analyzed teachers’ teaching practices in terms of the mathematical approach, and suggested an extension of Shulman’s (1986) categorizations of PCK and SMK. But, what caught our attention and interest was there were very few examples of what HCK really meant, and they also clearly indicated that:

We have no evidence that such mathematical perspective produces improvements in teachers’ effectiveness or in pupils’ learning. We do not know how to estimate how far out or in what direction the pedagogically relevant and useful horizon extends. We do not know the level of detail that is needed for horizon knowledge to be useful (Ball and Bass, 2009, p. 11).

Recently, some researchers (e.g., Figueiras et al., 2011; Foster, 2011; Vale et al., 2011; Zazkis and Momolo, 2011) have proposed their own meanings of HCK, and these meanings helped us deepen our understanding about HCK. However, we thought that their discourse and instantiation did not correspond to an important aspect that Ball and Bass (2009) mentioned:

“Felix Klein offered the attractive and oft-cited idea of a higher perspective on elementary mathematics. Our notion of horizon knowledge complements his. We hypothesize it as a kind of elementary perspective on advanced knowledge that equips teachers with a broader and also more particular vision and orientation for their work (Ball and Bass, p. 10).”

That is to say, if a teacher with rich mathematical knowledge could not transform the mathematical knowledge into the pedagogically useful forms, or could not lead their students to appreciate the structure and aesthetics of mathematics based on certain kind of elementary perspective on advanced knowledge, this kind of mathematical knowledge used in teaching should not be involved with MKT. Accordingly, we thought that a mathematics teacher with HCK might be able to penetrate through the structure of mathematics in terms of the fundamental ideas in mathematics. Moreover, teachers would be able to focus on significant content and to seek to fashion fruitful representational contexts for students to explore them (Ball, 1993). This line of argument implies that HCK might be a reciprocal pathway between the elementary and advanced mathematical knowledge. Here, in the following paragraph, we will conceive HCK as a complement of elementary-and-advanced aspect based on Ball and her colleagues’ suggestions.

HCK-awareness or Understanding

In order to understand more about this complementary aspect, we had been searching for the relevant journal articles, conference proceedings and conference presentations given by Ball and her colleagues. Then we grasped some ideas of HCK by looking at these materials chronologically.

At first, in 2008, HCK was described as “an awareness of how mathematical topics are related over the span of mathematics included in the curriculum” (Ball et al., p. 403). Here, we thought there might be some differences between this subcategory of SMK and the subcategory KCC of PCK. Vale et al. (2011) provided a professional learning program for teachers of junior secondary mathematics with regard to the content and pedagogy of senior secondary mathematics. They analyzed teachers’ reflections on their learning to explore teachers’ understanding of mathematical connections and their awareness of mathematical structure, and verified that this kind of connections in mathematical structure was unquestioningly beyond connections in curriculum. Moreover, they found that, if teachers were able to deepen and broaden their knowledge and could be aware of the mathematical structure, then their practices would support their students’ present and future learning of mathematics. Hence, this kind of the teachers’ deeper and broader mathematical knowledge can be used to develop their HCK and will afford their students to learn more mathematical connections.

Secondly, in March 2009, HCK was defined as “an awareness–more as an experienced and appreciative tourist than as a tour guide–of the large mathematical landscape in which the present experience and instruction is situated” (Ball and Bass, p. 6). They thought that a mathematics teacher who should be like an experienced and appreciative tourist gives students opportunities to explore more unknown journeys and to make connections among the known and unknown ones. And a teacher who can pay attention to where the students conceptually are can challenge and extend students’ thinking and modify or develop appropriate activities for students (Even and Tirosh, 1995). Namely, it is not sufficient that a mathematics teacher merely provides soluble, brilliant or even advanced approaches in dealing with mathematical problems, but does not trace problem-solving trajectories in terms of the students’ pre-conceptions. A mathematics teacher, not like a pedant, should create a mathematics sense-making learning environment (Lee and Lin, 1998) and should lead his or her students to explore the large mathematical landscape. Figueiras et al. (2011) indicated that, regardless of the learning of primary or secondary students, mathematics teachers require a much broader perspective on the nature of knowledge grounded in the coherence of mathematics. Moreover, they thought teachers’ learning of advanced mathematics should be subordinated in the mathematical education, because advanced mathematical knowledge would not be directly applied in teaching situations. However, they argued that teachers’ learning of the advanced mathematical knowledge is an essential ingredient for a deep understanding of basic mathematics. Hence, the mathematics teacher’s advanced mathematical knowledge is maybe just part of one’s HCK. Their HCK has to include a certain kind of pedagogically useful transformation upheld by the interactions between advanced and elementary mathematical knowledge.

Thirdly, in July 2009, HCK was defined as:

“the understanding of the broader set of mathematical ideas to which a particular idea. It is the sort of understanding that gives teachers peripheral vision for where they are and where their pupils are heading, to be conscious of the consequences of how ideas are represented, or the later development that is enabled- or possibly impeded- by decisions within the current work (Ball et al., p. 1-98).”

Here, we tried to understand these descriptions based on Ma’s (1996) framework. She divided teachers’ understanding of the topic of the subject into four different levels that included procedural understanding, conceptual understanding, logical relation and structure of the subject. She indicated that most experienced mathematics teachers could reach to the third level, and that only few might approach to the forth one. The forth level involves the basic principle and basic attitude. The basic principle refers to the principle which sustains many different concepts of the mathematical topic, but does not appear in each topic; and, the basic attitude maintains the penetrating characteristics among different mathematical topics, and embodies the consistency. Furthermore, for the mathematics teachers who can reach the forth level, they can exhibit connectedness, multiple perspectives, longitudinal coherence and the basics in their teaching and self-learning. In particular, the basics refer to the simple but powerful example that can help students learn. On the other hand, Chinnappan and Lawson (2005) compared two experienced high-school mathematics teachers’ teaching in geometrical content. They indicated that the connectedness of teachers’ knowledge was related to the understanding of knowledge, and relevant to quality of teaching. The richness of connection helps children make connections with their previous understandings and experiences. Therefore, if the simple but powerful example, besides helping students’ learning, also provides more profound connection, such example could be used as the mediator connecting to broader and deeper mathematical landscape.

We thought of HCK as mathematics teachers’ awareness or understanding based on the understanding of elementary mathematics. Such understanding can help teachers transform their knowledge into pedagogically useful forms based on students’ pre-conceptions, and these forms might be used to illuminate a kind of mathematical peripheral vision, a view of the larger mathematical landscape that teaching requires. In next section, we give a shared classroom teaching incidence to illustrate our aspect of HCK.

A SHARED CLASSROOM TEACHING INCIDENCE – THE MINIMAL VALUE OF VOLUME TETRAHEDRON

The problem in Figure 1 for the topic of the intercept form of plane equation in space was used by the three teacher cases. Their teaching practices were observed, video-recorded and analyzed by our research group. Each of them arranged different sequences to introduce the intercept form of plane equation and reviewed related pre-concepts to accomplish this task. Hence, we divided each case into the three parts to report the three stages of the teacher’s teaching practices in this section, including the introduction of major task or concept, teacher-self illustrations, and teacher’s further explanations or students explorations.

Introduction of Major Task or Concept

At first, Teacher A’s teaching practice presented the broken fragment in this part, because, at the beginning, he told his students: “the intercept form of plane equation is an independent but not a special unit (classroom teaching, Teacher A).” He then gave the generalized question: “A plane E passes through A (a, 0, 0), B (0, b, 0) and C (0, 0, c), and \(\text{abc} \neq 0\). Find the equation of plane E.” Moreover, he used the above-mentioned problem in Figure 1, followed by exploring the solving approach of this problem to be quite fixed, and told his students that he would give a quick but very trick way to solve it afterward. Then, he recalled the formula of volume of pyramid and asked students to memorize it, and immediately explained that the volume of tetrahedron OABC was equal to\(\ \left( \frac{1}{6} \right)\left| \text{abc} \right|\), as the plane E cuts the coordinate half-axes at points A(a, 0, 0), B(0, b, 0) and C(0, 0, c) and O is the origin point. He brought up the 3-variables arithmetic-geometric mean inequality, and told his students this inequality can be extended to n-variables; but he did not explain why. Finally, he solved this problem in terms of the formula of the volume of tetrahedron and 3-variables arithmetic-geometric mean inequality. It seemed to us that teacher A merely provided a teacher-proof solving strategy.

Teacher B, however, seemed to be a bit different from Teacher A. He reviewed two different representative forms of equation of plane in space, including general form and point-normal form; and then, he asked students to recall seven different representative forms of equation of line in plane, including general form, two points form, point-intercept form, point-slope form, slope-intercept form, intercept form and point-normal form. He led students to think about whether the concept of slope is needed in plane in space according to the students’ understanding of equation of line in plane, and, then, asked them to describe how to make distinction between the geometrical meanings of point-normal and intercept form of the plane equation. It is very clear that, in terms of the above-mentioned teaching activities, he wanted to convey and to explain the analogical relationship between the equations of line in plane and plane in space, and, furthermore, brought up the necessity of existence of intercept form. Although his latter teaching step was almost the same as Teacher A, but he at least gave students opportunities to recall the understanding and connection of intercept form. Certainly, for his students, the intercept form was not an independent unit.

By contrast, Teacher C provided more opportunities to elicit students’ thinking and presented different connections in this teaching incidence. At first, he offered the following question:” A plane E passes through A (2, 0, 0), B (0, 3, 0) and C (0, 0, 4), and O is the origin point. Find the equation of plane E and the volume of tetrahedron OABC” and students in the classroom were asked to think and solve the problem. He, following to this question, introduced the intercept form of plane equation in space by reviewing the intercept form of line equation in plane and by extending the definition of intercept to 3-D space. Moreover, he tried to explain the formula of tetrahedron volume which the students had learned. First, about recalling the volume formula of pyramid, he explained the relationship between cuboid and parallelepiped. In particular, borrowing few collecting students’ textbooks a little bit, he piled up and pushed them, and explained this relationship in the light of the Zu Chongzhi’s theory (or called Cavalieri’s principle). This teaching task dealt with the following relationship–the sections made by planes parallel to and at the same distance from their respective bases are always equal under the condition of two solids of equal altitude. Second, he explained the formula of volume of pyramid in terms of the school-provided teaching material. Third, he explained the three-variables arithmetic-geometric mean inequality according to the factorization of\(\ a^{3} + b^{3} + c^{3} - 3\text{abc}\), and claimed that n-variables one would be learned later in the third-grade high-school curriculum. Finally, he brought up the following problem in Figure 2 (The Minimal Area Problem) which the students had learned in first grade:

Figure 2. The minimal value of area of triangle OAB

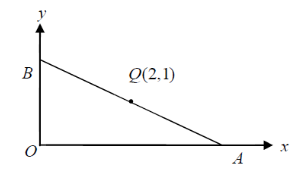
A line L passes through Q(2, 1) and cuts the positive coordinate half-axes at points A and B, and O is the origin point,

1. Find the minimum value of the area of the triangle OAB, and

2. Determine the equation of the plane that cuts this least area.

Students were asked to think about what relations between the problems in Figure 1 and in Figure 2 might be, and, would it be possible to solve the two problems by using similar approach. Therefore, Teacher C, in the connections of concepts, not only provided more explorations, but also offered more clear explanations by using practical and tangible examples. In the aspect of problem-solving strategy, he reinforced the connections and coherence between solving strategies of these two problems. In next section, we described their owned professions about the incidence.

Teacher-self Illustrations and Student Explorations

The three teachers, after providing demonstrating their strategies, solved the problem in Figure 1 almost with the same procedure as follows:

Let the equation of the plane E be \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) which passes through P(2,1,3), then we have \(\frac{2}{a} + \frac{1}{b} + \frac{3}{c} = 1\). Using the arithmetic-geometric mean inequality, we get the inequality\(\ \frac{1}{3}\left( \frac{2}{a} + \frac{1}{b} + \frac{3}{c} \right) \geq \sqrt[3]{\frac{2}{a} \cdot \frac{1}{b} \cdot \frac{3}{c}}\). Since the formula of the volume of the tetrahedron OABC is\(\ \frac{1}{6}\text{abc}\), and let\(\ V = \frac{1}{6}\text{abc}\). Therefore, \(\frac{1}{3} \geq \sqrt[3]{\frac{6}{6V}} = \sqrt[3]{\frac{1}{V}}\), then\(\ V \geq 27\). Latter, when\(\ \frac{2}{a} = \frac{1}{b} = \frac{3}{c} = \frac{1}{3}\), the equality holds. That is to say, when\(\ a = 6\), \(b = 3\) and \(c = 9\), the equation of the desired plane is\(\ \frac{x}{6} + \frac{y}{3} + \frac{z}{9} = 1\).

After that, they offered more or less different explorations or explanations further for the problem as following in their classroom teaching:

Teacher A: Now, let us replace 2, 1 and 3 with\(x_{0}\), \(y_{0}\) and \(z_{0}\) respectively, by the same token, we have \(V \geq \left( \frac{9}{2} \right)x_{0}y_{0}z_{0}\), \(a = 3x_{0}\), \(b = 3y_{0}\), \(c = 3z_{0}\ \)and the equation of the plane becomes \(\frac{x}{3x_{0}} + \frac{y}{3y_{0}} + \frac{z}{3z_{0}} = 1\). Noticing that the minimal volume of the tetrahedron OABC is \(\left( \frac{1}{6} \right)(3x_{0})(3y_{0})(3z_{0})\). Did you see that the answers of these kinds of problems are very easily to get…I personally thought that these kinds of problems are meaningless and worthless, but many teachers liked to use it to test their students…please you find the answer if point P is (2, -1, 3).

Teacher B: Ah… I wished that you could think about different solving methods, OK? Moreover, did you find that point P and points A, B and C has a specific mathematical relationship, while the volume of the tetrahedron OABC which passes through P is always the minimal value?

Teacher C: Note! Did you find that the arithmetic-geometric mean inequality is a useful tool to deal with the problem of extreme values? Your understanding of the mathematical relationship between intercept form of plane equation and arithmetic-geometric mean inequality will be able to be deepened by thinking and solving such as a good problem.

However, concerning their offering of self-explanations and student explorations, what kinds of the mathematical knowledge did the teachers actually use or understand, or what were they aware of? In general, Mr. Chiu, after watching their videotapes, provided some suggestions based on the purpose of the high-school curriculum and student learning. However, he yet pointed out few shortcomings such as the teachers did not lead students to explore the fundamentally geometrical relation of points P and Q in relation to the concept of arithmetic-geometric mean inequality, the definition of intercept form of linear equation and the definition of area and volume; furthermore, he showed a teaching illustration concerning the problems in Figure 1 based on his understanding of advanced mathematical knowledge in Table 1, and illustrated how his understanding of the advanced mathematical knowledge was used in teaching. In next section, we describe his teaching illustration on this issue.

Mr. Chiu’s Teaching Illustrations

Among the three teachers’ teaching incidences, Mr. Chiu appreciated and approved of the Teacher C’s teaching connection between the problems in Figure 1 and in Figure 2 according to the same solving strategies. However, for Mr. Chiu, the limitations of these teaching incidences are apparent because all the three teachers did not provide the students’ explorations of the mathematically geometrical relevance of the points P and Q. Mr. Chiu thought that this is a good opportunity to lead students to explore the concepts of volume and centroid in abstract 4-D space from them in 3-D Euclidean spaces. Therefore, he provided a teaching illustration divided into three levels with reference to the Figure 3.

Figure 3. The three level of Mr. Chiu’s teaching illustration

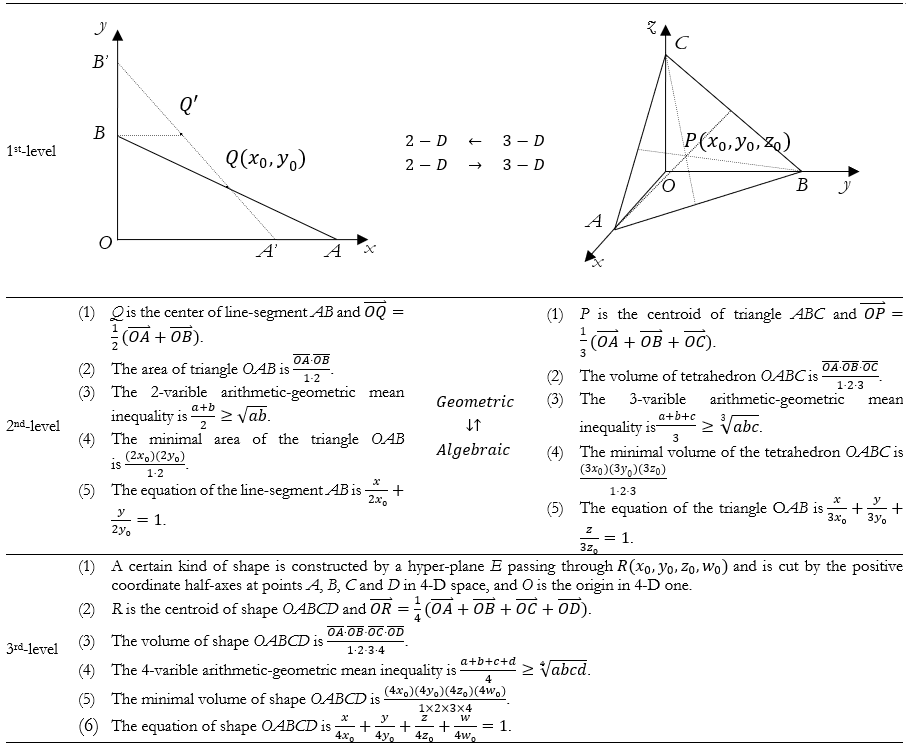
We described the first level of Mr. Chiu’s teaching illustration as the ‘elementary-to-advanced’ one. This level is about review of the geometric features. He thought it is necessary to review the plane Euclidean geometry learned by students in junior high-school and the fundamentally geometric features in 2-D and in 3-D spaces. Firstly, he gave the first geometrical proposition as “Q is the center of line-segment AB if and only if the area of triangle OAB is minimal”. He thought the majority of students are able to complete this proof with the geometrical approach, or dropped two hints: “Q is the center of line-segment AB but is not one of line-segment \(A'B'\) if and only if the area of triangle \(\text{OA}'B'\) is bigger than the area of triangle OAB” and “\(Q'\) is a point of line-segment \(A'B'\) and \(\text{BQ}'\) parallels x-axis”. Secondly, Mr. Chiu asked students to think about the relationship between geometric meanings of center in line-segment andcentroid in triangle. Namely, it is important to know the centroid of triangle to be the intersection of three medians. Finally, Mr. Chiu provided the second geometrical proposition as “P is the centroid of triangle ABC if and only if the volume of the tetrahedron OABC is minimal”. He asked students to prove it in terms of the above-mentioned geometric features and propositions.

About the second level, we described it as the ‘peripheral’ one. This level is about the algebraic representations of the equation of line in plane and plane in space, center in line-segment, centroid in triangle, area of the triangle, volume of the tetrahedron, intercept form of line equation in plane and in space, and arithmetic-geometric mean inequality. Mr. Chiu thought, in this level, students must be asked to observe the analogical relationship between center in line-segment and centroid in triangle, between area of the triangle and volume of the tetrahedron, between intercept form of line equation in plane and in space and between 2-varibles and 3-varibles arithmetic-geometric mean inequality. Furthermore, during this observation, he asked students to think about the constructive process of coordinate system from 2-D to 3-D. This is a key point, for him, about how to construct the 4-D coordinate system from analogical relationship between algebraic representations and geometric meanings in 2-D and 3-D Euclidean spaces. Mr. Chiu thought that, for some students, it is simple to observe this relationship.

The third level is described as the ‘horizontal’ one involving with the construction of the abstract space, but Mr. Chiu knew not all students could reach this level. Mr. Chiu led students to think the construction of 4-D space in terms of algebraic and geometric aspects. Firstly, he thought, it is important to define the geometric meaning of linear equation to be the hyper-plane in 4-D space. Secondly, he led students to image a certain kind of shape constructed by a hyper-plane E passing through \(R(x_{0},y_{0},z_{0},w_{0})\) and cut by the positive coordinate half-axes at points A, B, C and D in 4-D space. Thirdly, it is important to define the volume of this kind of shape OABCD, as O is the origin in 4-D space, and Mr. Chiu gave the following problem to find the minimum value of the volume of this kind of shape OABCD and to determine the equation of the hyper-plane that cuts this least volume. He thought, if students can reach this level, they might be able to extend the result to n-D space.

Mr. Chiu claimed that it is important to understand the fundamental mathematical meanings of the definition in the advanced mathematics, and, more significantly, to provide students opportunities to approach such meanings in exploring and connecting to the future mathematical journey or the advanced mathematical knowledge. We felt that the quality of the connectedness of Mr. Chiu’s mathematical knowledge seemed higher and deeper than the three participant teachers according to his understanding of advanced mathematics. Later, concerning the fundamental meaning of point P in Figure 1 and the related mathematical knowledge in Table 1, we interviewed the three participant teachers and hoped to examine whether they were aware of such quality of mathematical connection, and attempting to bring out the complementary aspect of HCK.

Teacher A: This point P is the centroid of triangle ABC, isn’t it? But I was not sure whether this characteristic is so important…Oh! Really! However, I thought that, for my students, it is enough if they could solve this problem quickly, because they will learn the n-varibles arithmetic-geometric mean inequality in next year.

Teacher B: The point P is the centroid of triangle ABC! As for the importance of this point P… I really did not know, and I just knew this is a brilliant approach to solve this problem. You said if we knew the definition of centroid and volume in n-dimensional space, you would have had…that’s right!

Teacher C: I really did not know what characteristic the point P hold, could you tell me more about… it is the centroid of triangle ABC. And then…according to the definition of the centroid and volume in n-D space, and n-varibles arithmetic-geometric mean inequality…that’s right! I never thought that. Wow! This idea is too important. I should include this aspect in the future.

All of these three participant teachers did not know the related advanced mathematics in Table 1, and one of them did not entirely know the fundamental characteristic of the point P. But they had been aware of its importance in mathematics. One of them immediately considered using this idea in next year teaching, namely, the connectedness presented by their teaching practice should be relevant to their awareness or understanding of advanced mathematical knowledge. In next section, we would re-conceptualize HCK from this aspect.

THE RE-CONCEPTUALIZATION OF HCK

The above teaching incidence collected from the three participant teachers, together with Mr. Chiu’s insightful teaching illustration, seems to meet the following four constituent elements of HCK (Ball and Bass, 2009, p. 5):

1. A sense of the mathematical environment surrounding the current “location” in instruction

2. Major disciplinary ideas and structures

3. Key mathematical practices

4. Core mathematical values and sensibilities

Mr. Chiu understood that this problem task is an important teaching example for the topic in the present and for students’ future mathematical journey, and he was also aware of the relationship between this problem and the problem in Figure 2 considering from the concept of center and centroid in relation to the intercept form of linear equation, arithmetic-geometric mean inequality and definition of area and volume. Hence, a mathematics teacher’s understanding of these mathematical definitions and connections embedded in the essence of mathematical structure is not only important for teaching, but also generative for student learning. Such understanding might help mathematics teachers deepen and broaden their thinking and practice, and also lead students to understand and be aware of the larger mathematical landscape.

We propose a complementary aspect which conceives mathematics teachers’ HCK from the elementary-to-advanced point of view. We define the elementary mathematical knowledge as those fundamentally mathematical meaning (e.g., the concept of center and centroid) embedded in the advanced level. With this aspect of HCK, a mathematics teacher’s understanding or awareness of mathematical horizon will be more penetrative, in other word, more “connected, coherent and basic”(Ma, 1996). We suggest teachers’ HCK as a reciprocal navigating pathway between the elementary and the advanced aspect of mathematical knowledge in Figure 4.

Figure 4. Horizon content knowledge: A complementary aspect

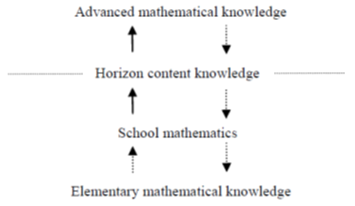
Namely, HCK can help mathematics teachers’ to think back and forth between elementary and advanced mathematical knowledge. However, Foster (2011, p. 24) suggested that what peripheral mathematical knowledge a mathematics teacher needs is mathematical rather than pedagogical, it can also be thought of as an applied mathematics where the application is teaching. He introduced some examples which are useful for teaching. For example, \(tan35^{\circ}\) is very close to 0.7. Mathematics teachers know that long before such knowledge is applied in teaching, and they also know that their students should have learned the definitions and related properties of trigonometric functions in the case of right-angled triangle. The function \(\tan\theta\) is increasing for \(\theta\) increases from \(0^{\circ}\) to \(90^{\circ}\). Teachers could lead students to think what value \(tan35^{\circ}\) will be approaching to, for \(30^{\circ} < \theta < 37^{\circ}\), where \(\theta = 37^{\circ}\) is an angle in right-angled triangle with two sides 3 and 4 and hypotenuse 5. Therefore, such knowledge is not only mathematical but also pedagogical. On the other hand, some examples given by Zazkis and Mamolo (2011) were related to HCK, but these examples did not conform to all four constituent elements of HCK. For example, the mathematics teacher recognized the prime factorization of 180 as \(2^{2} \times 3^{2} \times 5\) and, based on the fundamental principle of counting in discrete mathematics at college, concluded that the number of factors was \(3 \times 3 \times 2\). This teacher did not intend to teach his students this principle, so this knowledge related merely to major disciplinary ideas and structure of numbers. However, we suggestthe teaching illustration presented by the Figure 5, which can meet the four constituent elements of HCK. We think that the arborescence is the fundamental feature of the counting in discrete mathematics, so the arborescence is not only major disciplinary ideas and structure, but also core mathematical values and sensibilities. Moreover, it is used more suitably in the mathematics teacher’s teaching practice that will lead students to explore the fundamental principle of counting. Thus, our teaching illustration expands Zazkis and Mamolo’s idea, and embody that if teachers do not transform “the advanced” into pedagogically useful forms based on students’ pre-conception and its fundamentally mathematical features, such knowledge is likely not to belong to HCK. Therefore, we suggest that, besides requiring a much broader or advanced perspective on the nature of knowledge (Figueiras el at., 2011, p. 28), mathematics teachers need also deepen their own knowledge based on re-examining the understanding of the fundamental meaning of concept from the elementary-to-advanced aspect. Such understanding or awareness of HCK, will not only complement Klein’s advanced-on-elementary aspect, but also facilitate students’ learning of the larger mathematical landscape.

Figure 5. The teaching illustration of the fundamental principle of counting

FOOTNOTE

The term fundamental has three related meanings: foundational, primary, and elementary. Mathematics is an area of science that concerns spatial and numerical relationships in which reasoning is based on these relationships…None of the new branches, whether pure or applied, operates without the basic mathematical rules and computational skills established in arithmetic and geometry. Elementary school mathematics, composed of arithmetic and primary geometry, is therefore the foundation of the discipline on which advanced branches are constructed. The term primary refers to another feature of elementary mathematics. Elementary mathematics contains the rudiments of many important concepts in more advanced branches of the discipline…The foundational and primary features of mathematics, however, are presented in an elementary format. It is elementary because it is at the beginning of students’ learning of mathematics (Ma, 1999, p. 116-117).